EUCLID (Efficient Unsupervised Constitutive Law Identification & Discovery) is here applied to discover path-dependent material behavior, i.e., elastoplastic material models and generalized standard material models.

Elastoplasticity

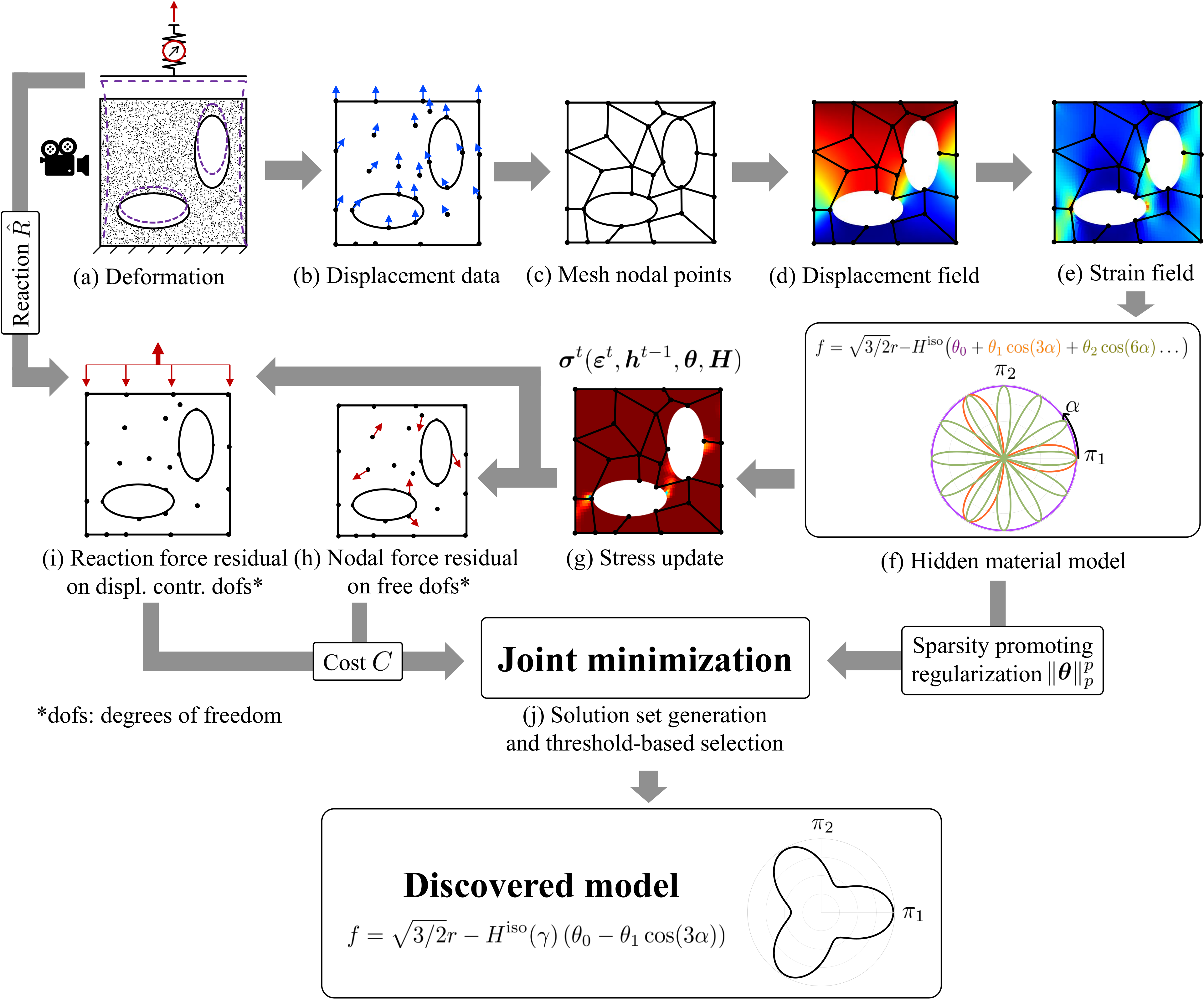
In a single experiment with complex geometry (a), point-wise displacements (b) and global reaction forces (i) are measured. A quadrilateral finite element mesh is constructed (c) to interpolate the displacement data. The resulting displacement field (d) is differentiated to arrive at the strain field (e). The material model library (f) is constructed (here based on a Fourier ansatz). Based on this library and for given material parameters theta and H, the stresses can be calculated by applying a classical elastic predictor - plastic corrector return mapping algorithm at each load step in the data set, while the history variables are updated at each step (g). Based on the stresses, the internal and external virtual works and hence the internal (h) and external (i) force imbalances are calculated, contributing to the cost function. Finally, the cost function is minimized jointly with a sparsity promoting regularization term (j) to generate a set of solutions out of which a solution with low cost and high parsimony is automatically selected.

Generalized standard materials

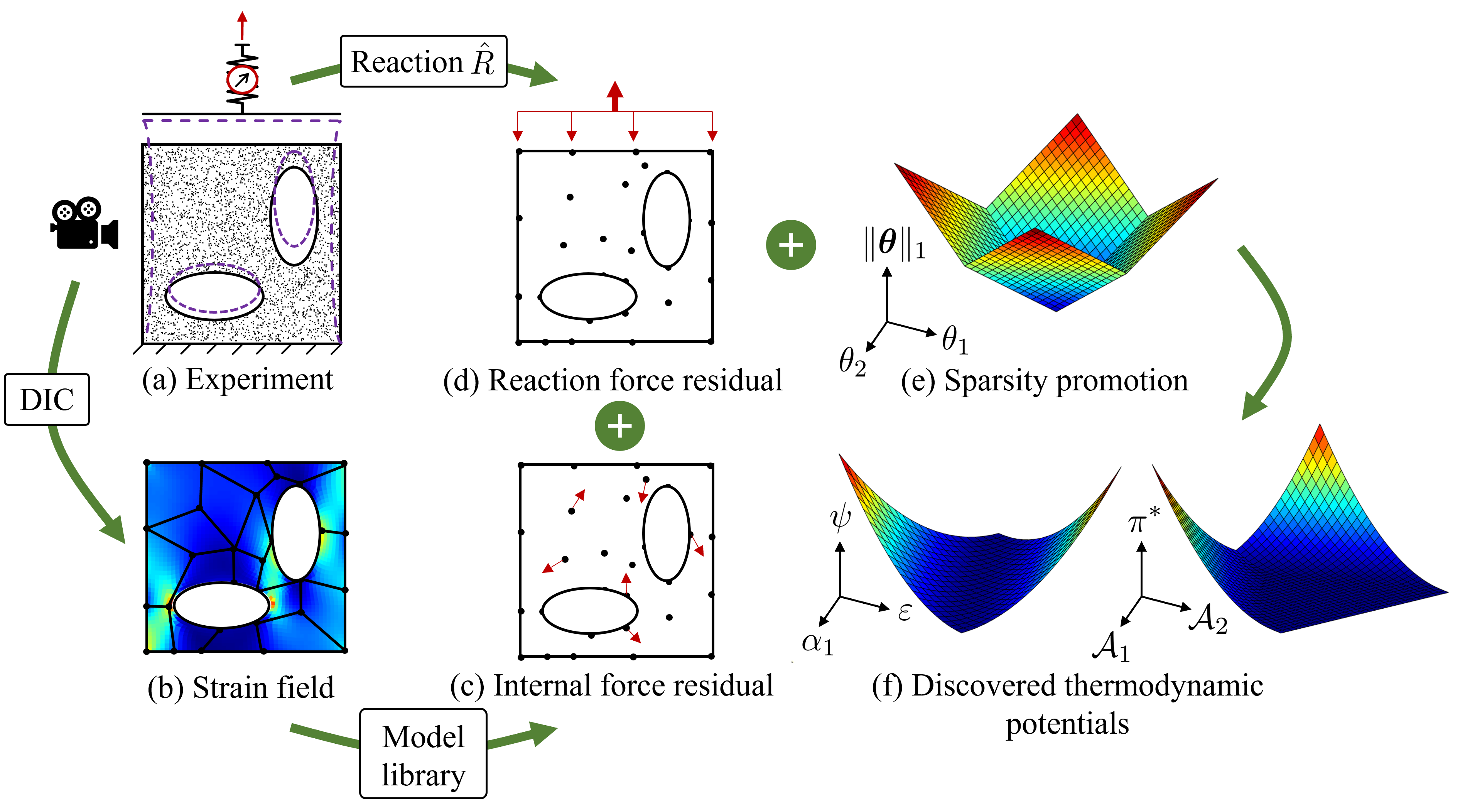
From a mechanical test on a specimen with complex shape (a), the strain field over the specimen surface is acquired using digital image correlation (DIC) (b) , and the reaction force at the boundary is measured using a load cell. Introducing a model library, the residuals of the weak form of linear momentum balance in the interior (c) and at the boundary (d) can be expressed as functions of the material parameters theta. By minimizing the sum of squared residuals of the linear momentum balance along with a sparsity promoting regularization term (e), the thermodynamic potentials (f) are discovered as parsimonious mathematical formulae.

Corrigendum

Please note a slight misuse of notation in the paper. Both the short-term moduli (G0, K0 in the code) and long-term moduli (Ginf, Kinf in the code) are denoted as G, K in the paper. In Eq. (13), Eq. (17), and in all equations in the appendix, the long-term moduli are considered, i.e., G, K correspond to Ginf, Kinf. In Eq. (25) and Table 2, the short-term moduli are considered, i.e., G, K correspond to G0, K0. It is G0 = Ginf + sum(Gi) and K0 = Kinf + sum(Ki).

About the documentation

The documentation contains detailed information for the most important functions (subroutines). For each function, the input arguments and output arguments are provided. The documentation can be browsed by using the search box. The provided examples help to understand the workflow of EUCLID, they can be executed using the provided codes and data.