EUCLID-code
Introduction
EUCLID (Efficient Unsupervised Constitutive Law Identification & Discovery) utilizes local displacement and global reaction force data, but no local stress data as these are not available from experiments, to discover material models without assuming a specific functional form for the model a priori. To this end, a large catalog of candidate material models is constructed out of which dominant candidates are selected through sparse regression or the material behavior is described by a general machine learning based ansatz, e.g., a neural network. To compensate the unavailability of stress data, physics knowledge is employed by minimizing the sum of squared residuals of the weak linear momentum balance.
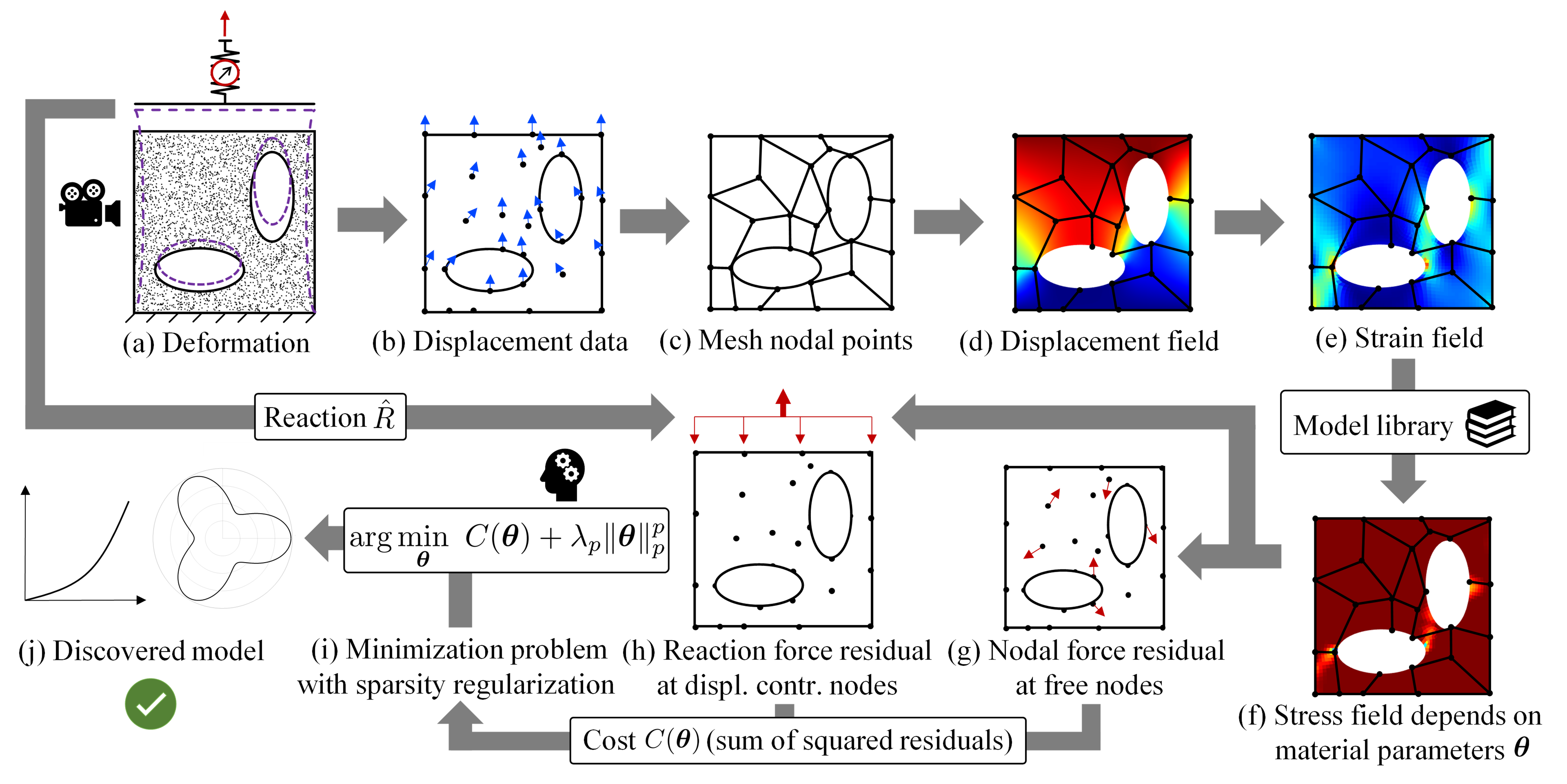
Figure 1: EUCLID workflow.
The figure above shows the workflow of the sparse regression based EUCLID algorithm.
Full-field displacement and net reaction force data that are obtained from a single experiment (a) serve as input data for EUCLID.
The displacement data (b) is interpolated (c) to obtain the displacement field (d) and after differentiation the strain field (e).
A general material model library is constructed, which can describe a variety of different material responses dependent on the choice of material parameters theta.
Based on the model library, the stresses (f) and hence the residuals of the weak linear momentum balance (g,h) can be expressed dependent on the unknown parameters theta.
The linear momentum balance serves as a physical constraint on the material parameter space.
Minimizing the sum of squared residuals together with a sparsity promoting regularization term (i) yields a sparse parameter vector theta
and hence an interpretable constitutive law expressed by a compact mathematical formula (j).
Applications
Hyperelasticity
EUCLID was successfully demonstrated to be able to discover strain energy density functions of hyperelastic materials (see Ref. 1.). The codes and data are publically available on GitHub (see Ref. 2.) and the ETH Research Collection (see Ref. 3.), respectively. The documentation of the hyperelasticity code and an example can be found here.
Experimental Validation
An experimental validation of EUCLID for the automated discovery of strain energy density functions of human brain tissue is presented in Ref. 13. As the shiny surface of human brain tissue is not suited for full-field displacement measurements, a supervised version of EUCLID is proposed (in contrast to the original unsupervised concept of EUCLID), which is informed by labelled stress-strain and torque-twist data pairs. Codes are publically available in the ETH Library (see Ref. 14.).
Bayesian Inference
In Ref. 7., the problem of material model discovery was considered from a Bayesian perspective. Through Markov Chain Monte Carlo sampling, the Bayesian-EUCLID deduces a posterior probability distribution for the unknown material parameters, which is a joined distribution of the model likelihood and a sparsity promoting spike-and-slab prior. In this way, parsimonious and interpretable material models can be discovered with quantifiable uncertainties. The codes and data are publically available on GitHub. The documentation of the Bayesian-EUCLID code and an example can be found here.
Neural networks
In Ref. 8, we demonstrate the use of neural networks for learning the hidden material models from full-field displacement and global reaction force data. By using an Input Convex Neural Network (ICNN) and a physics guided training protocol, we ensure that the learned strain-stress relation fulfills multiple physical constraints. Moreover, we present the capability of our ICNN-based material model to learn the hidden fiber angle arrangments of anisotropic hyperelastic materials. The codes and data are publically available on GitHub (see Ref. 8.). The documentation of the NN-EUCLID code and an example can be found here.
In Ref. 17, we present the Input-Convex Kolmogorov-Arnold Networks (ICKANs) architecture for constitutive modeling of hyperelasticity within the NN-EUCLID framework. Compared to ICNNs and other black-box models, ICKANs offer improved interpretability in capturing constitutive behavior. Additionally, we employ a model distillation strategy that combines input-convex symbolic regression with the Kolmogorov-Arnold representation theorem, resulting in fully interpretable, analytical constitutive models. The codes and data are publically available on GitHub (see Ref. 17).
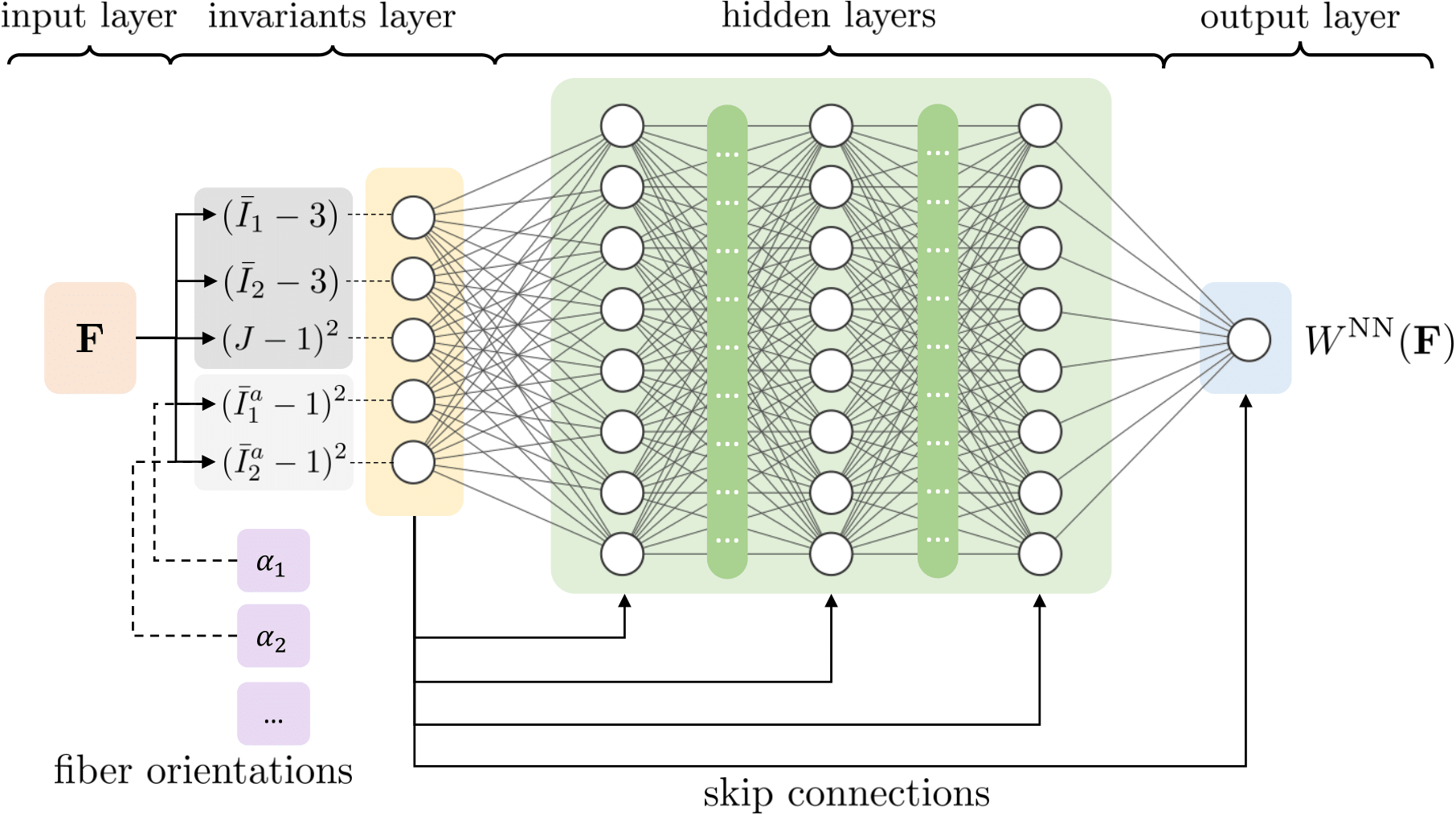
Figure 2: Neural network.
Viscoelasticity
In Ref. 11, EUCLID is used to identify the material model of a viscoelastic material from full-field displacement and reaction force data in the frequency domain. Starting from a large library of viscoelastic Maxwell elements, EUCLID automatically selects the most relevant elements using sparse regression and k-means clustering. The codes are publically available on GitHub.
Elasto-Plasticity
In Ref. 4., EUCLID was for the first time applied to discover elasto-plastic material models. Full-field displacement and global reaction force data are used to discover plastic yield surfaces and hardening laws as closed-form mathematical formulas (see Animation 1). The codes and data are publically available on GitHub (see Ref. 5.) and the ETH Research Collection (see Ref. 6.), respectively. The documentation of the elasto-plasticity code and an example can be found here. An extention to non-associated pressure-sensitive plasticity is presented in Ref. 18.
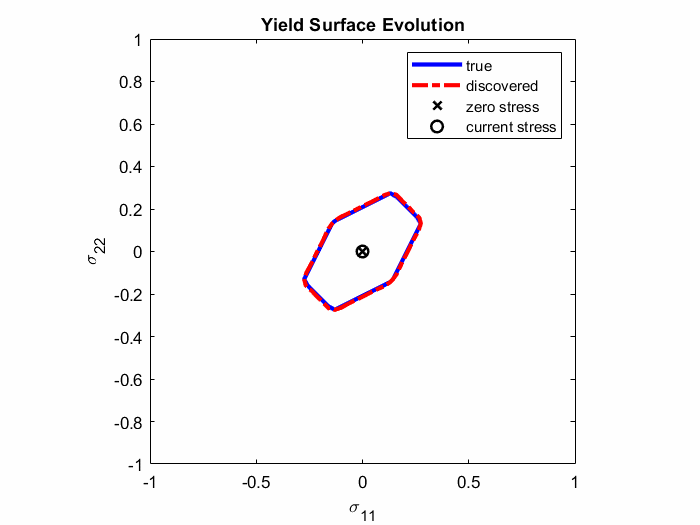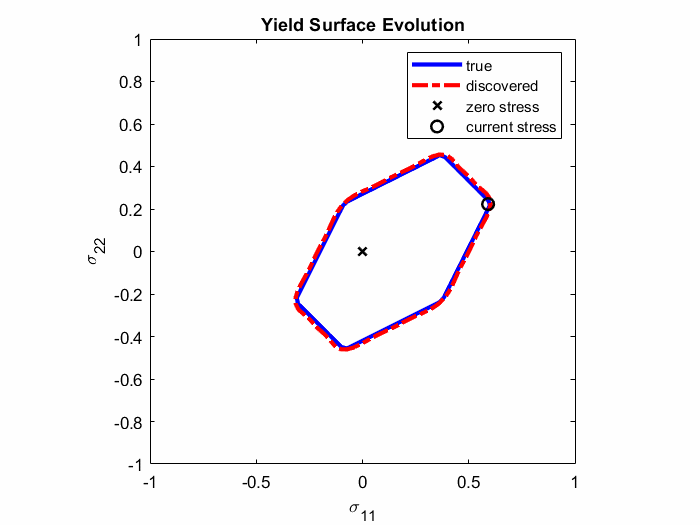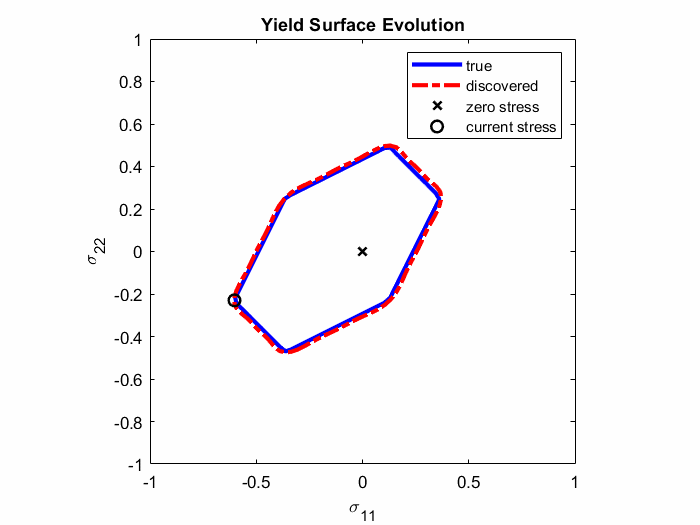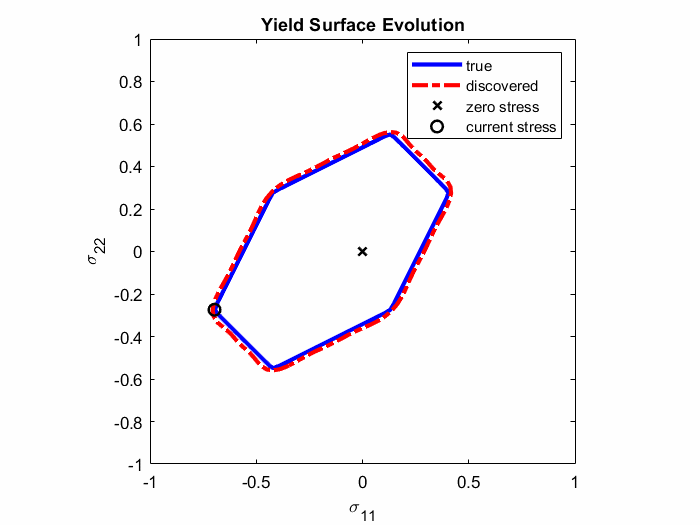
Animation 1: Comparison between the true and discovered yield surface evolution along a given deformation path.
Generalized Standard Materials
In Ref. 9., the EUCLID framework is extended to generalized standard materials. In this way, no a priori choice of a material class (such as hyperelasticity or elasto-plasticity) has to be made and EUCLID can automatically discover the true hidden material model from a large catalog of constitutive classes, including elasticity, viscoelasticity, elastoplasticity, viscoplasticity, isotropic and kinematic hardening. Codes (see Ref. 5.), data (see Ref. 10.), and a documentation are publically available.
Neural networks
In Ref. 15., we present a machine learning framework based on convex neural networks for learning the thermodynamic potentials of generalized standard materials. Codes (see Ref. 16.) are publically available.
References
-
Moritz Flaschel*, Siddhant Kumar* and Laura De Lorenzis (*contributed equally)
Unsupervised discovery of interpretable hyperelastic constitutive laws
Computer Methods in Applied Mechanics and Engineering, 381, p.113852 (open access) -
Moritz Flaschel*, Siddhant Kumar* and Laura De Lorenzis (*contributed equally)
Supplementary software for “Unsupervised discovery of interpretable hyperelastic constitutive laws”
ETH Library
DOI: http://doi.org/10.5905/ethz-1007-508
GitHub: https://github.com/EUCLID-code/EUCLID-hyperelasticity -
Moritz Flaschel*, Siddhant Kumar* and Laura De Lorenzis (*contributed equally)
FEM Data – Unsupervised discovery of interpretable hyperelastic constitutive laws
ETH Research Collection
DOI: https://doi.org/10.3929/ethz-b-000505693 -
Moritz Flaschel, Siddhant Kumar and Laura De Lorenzis
Discovering plasticity models without stress data
npj Computational Materials, 8, 91 (2022) (open access) -
Moritz Flaschel, Siddhant Kumar and Laura De Lorenzis
Supplementary software for “Discovering plasticity models without stress data”
ETH Library
DOI (version 1.0): http://doi.org/10.5905/ethz-1007-509
DOI (version 2.0): http://doi.org/10.5905/ethz-1007-605 (version 2.0 further includes the supplementary software for “Automated discovery of generalized standard material models with EUCLID”)
GitHub: https://github.com/EUCLID-code/EUCLID-plasticity -
Moritz Flaschel, Siddhant Kumar and Laura De Lorenzis
FEM Data - Discovering plasticity models without stress data
ETH Research Collection
DOI: https://doi.org/10.3929/ethz-b-000534002 -
Akshay Joshi, Prakash Thakolkaran, Yiwen Zheng, Maxime Escande, Moritz Flaschel, Laura De Lorenzis, Siddhant Kumar
Bayesian-EUCLID: discovering hyperelastic material laws with uncertainties
Computer Methods in Applied Mechanics and Engineering, 398, p.115225 (open access)
GitHub: https://github.com/EUCLID-code/EUCLID-hyperelasticity-bayesian -
Prakash Thakolkaran, Akshay Joshi, Yiwen Zheng, Moritz Flaschel, Laura De Lorenzis, Siddhant Kumar
NN-EUCLID: deep-learning hyperelasticity without stress data
Journal of the Mechanics and Physics of Solids, 169, p.105076 (open access)
GitHub: https://github.com/EUCLID-code/EUCLID-hyperelasticity-NN -
Moritz Flaschel, Siddhant Kumar, Laura De Lorenzis
Automated discovery of generalized standard material models with EUCLID
Computer Methods in Applied Mechanics and Engineering, 405, p.115867 (open access) -
Moritz Flaschel, Siddhant Kumar and Laura De Lorenzis
FEM Data - Automated discovery of generalized standard material models with EUCLID
ETH Research Collection
DOI: https://doi.org/10.3929/ethz-b-000586072 -
Enzo Marino, Moritz Flaschel, Siddhant Kumar and Laura De Lorenzis
Automated identification of linear viscoelastic constitutive laws with EUCLID
Mechanics of Materials, 181, p.104643 (open access preprint)
GitHub: https://github.com/EUCLID-code/EUCLID-viscoelasticity -
Moritz Flaschel
Automated Discovery of Material Models in Continuum Solid Mechanics
Ph.D. thesis (open access) -
Moritz Flaschel, Huitian Yu, Nina Reiter, Jan Hinrichsen, Silvia Budday, Paul Steinmann, Siddhant Kumar and Laura De Lorenzis
Automated discovery of interpretable hyperelastic material models for human brain tissue with EUCLID
Journal of the Mechanics and Physics of Solids, 180, p.105404 (open access) -
Huitian Yu, Moritz Flaschel and Laura De Lorenzis
Supplementary software for “Automated discovery of interpretable hyperelastic material models for human brain tissue with EUCLID”
ETH Library
DOI: https://doi.org/10.5905/ethz-1007-638 -
Moritz Flaschel, Paul Steinmann, Laura De Lorenzis and Ellen Kuhl
Convex Neural Networks Learn Generalized Standard Material Models
DOI: http://dx.doi.org/10.2139/ssrn.5023581 -
Moritz Flaschel, Paul Steinmann, Laura De Lorenzis and Ellen Kuhl
Supplementary software for “Convex Neural Networks Learn Generalized Standard Material Models”
DOI: http://doi.org/10.5281/zenodo.14055700
GitHub: https://github.com/mflaschel/GSMN -
Prakash Thakolkaran*, Yaqi Guo*, Shivam Saini, Mathias Peirlinck, Benjamin Alheit and Siddhant Kumar (*contributed equally)
Can KAN CANs? Input-convex Kolmogorov-Arnold Networks (KANs) as hyperelastic constitutive artificial neural networks (CANs)
Computer Methods in Applied Mechanics and Engineering, 443, p.118089 (open access)
GitHub: https://github.com/mmc-group/ICKANs -
Haotian Xu, Moritz Flaschel and Laura De Lorenzis
Discovering non-associated pressure-sensitive plasticity models with EUCLID
Advanced Modeling and Simulation in Engineering Sciences, 12, 1 (open access)
GitHub: https://https://github.com/EUCLID-code/EUCLID-plasticity-pressure-sensitive-non-associated